数式の記述フォーマット
Mathematicaはプログラム言語ですので、入力する数式に文法があります。
初めは戸惑うかもしれませんが、簡単に学べ一貫性のある文法です。
文法の注意
- アルファベットの大文字と小文字の区別
- Mathematicaの標準関数は全てアルファベットの大文字で始まる
- 関数の引数は、全て [...] のように角括弧で記述する
- 変数の変異などを指定するリストは、{...} のように中括弧で記述する
四則演算 (足し算、引き算、掛け算、割り算)
普通の四則演算を計算させるのは、至ってシンプルです。
四則演算のルール「乗算・除算」は、括弧がなくても優先して計算されます。
負の数を使った計算を行うこともできます。
記述文法
| + | 左辺と右辺の足し算を行います。 |
| - | 左辺と右辺の引き算を行います。 |
| * | 左辺と右辺の掛け算を行います。 |
| / | 左辺と右辺の割り算を行います。 |
| ( ) | 括弧内の数式を先に評価します。 |
数式のサンプル
|
1 2 3 4 5 6 7 |
1 + 2 2 - 5 3 * 5 10 / 2 2 * 3 + 5 (2 + 3) * 5 |
サンプルの評価結果

分数や小数を使った演算
分数は割り算と同じ「/ (スラッシュ)」を使って表し、小数は「. (ピリオド)」を使います。
また、どうしても分数を小数で表示したい場合のために N という関数が Mathematica に組込まれています。
記述文法
| / | 左辺に分子、右辺に分母の数値・数式を記述して分数を表現します。 |
| . | 左側に整数部、右側に小数部を記述して小数を表現します。 |
| N[<数式>, <桁数>] | 分数を小数で表示したい時に使用します。<桁数>は省略可能です。 |
数式のサンプル
|
1 2 3 4 5 6 |
2 / 3 2 / 3 * 3 / 5 N[2 / 3] N[2 / 3, 100] 3.14 * 10 |
サンプルの評価結果

ポイント
分数同士の計算を見ても分かるように、2÷3を電卓では0.666667として扱われるのに対し、Mathematicaでは分数として扱われているのが分かります。また、分数の約分もしっかり行われていますね。
べき乗と平方根(ルート)
べき乗を計算させるには、ハット記号「^」を使用します。
また、平方根の計算には Sqrt という Mathematica の組込み関数を使用します。
記述文法
| ^ | 左側に底、右側に指数を記述します。 |
| Sqrt[<数式>] | <数式>に平方根を求めたい数式・値を記述します。 |
数式のサンプル
|
1 2 3 |
2^10 3.14^30 |
サンプルの評価結果

ポイント
2つ目の評価結果では、科学計算の表記で出力されています。
これも分数と同じく、内部では切り捨てや四捨五入が行われているわけではありません。
一次・二次・高次・連立方程式を解く
一次方程式、二次方程式、連立方程式の解を求める関数として Solve がMathematicaに組込まれています。
記述文法
| = | 左辺の変数に右辺の値を代入します。 |
| =. | 等号(=)で代入した値をクリアします。 |
| == | 左辺と右辺が等しいかどうかを調べます。等式としても使用します。 |
| Solve[<方程式>, <解を求める変数>] | 方程式あるいは不等式の解を<解を求める変数>について求めます。 |
数式のサンプル
|
1 2 3 4 5 6 7 8 9 10 |
x = 5 x x == 5 x == 6 x =. x Solve[2x + 3 == 5, x] Solve[x^2 + 2x - 3 == 0, x] Solve[{x + y == 20, x - y == 5}, {x, y}] |
サンプルの評価結果
変数代入と等式

一次方程式、二次方程式、連立方程式の解法

展開と因数分解
数式を展開させる関数として、Expand と ExpandAll という関数がMathematicaに組込まれています。
また、因数分解をする関数として、Factor という関数が組込まれています。
記述文法
| Expand[<数式>] | <数式>を展開する。分数の場合は、分子のみを展開する。 |
| ExpandAll[<数式>] | <数式>を展開する。分数の場合は、分子と分母の全てを展開する。 |
| Factor[<数式>] | 多項式である<数式>を因数分解する。 |
| Together[<数式>] | 項の和を共通分母にあげ、その結果を因数約分する。 |
数式のサンプル
|
1 2 3 4 5 6 7 8 9 |
e = (x - 1)^2(2 + x)/((1 + x)(x - 3)^2) e Expand[e] ExpandAll[e] f = Expand[e] f Factor[f] Together[f] |
サンプルの評価結果
数式の展開

数式の因数分解
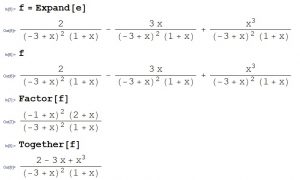
以上、「【基本】使ってみよう!四則演算から因数分解まで」でした。
